Algebraic patterns — Identity element
Posted on June 29, 2016Introduction
The Identity element pattern is all about defining the concept of emptiness, and is a good introduction to algebraically modelling programming concepts.
There are certain values — probably found scattered around the code
you’re working on right now — values like the numbers 1 and 0,
the empty string "" or the empty array [], that are often used as
initializers and somehow feel “empty” or uninteresting.
The identity element pattern allows us to formalize this notion in a
precise way, letting us explain just why these values are so
common. That is, in a given code base, you’re probably more likely to
see the string "", than say, the string "banana", and the number
0 more than the number 4279. Is there some way we can explain what
makes these values special?
Imagine an empty glass. How can we define what it means for a glass to be empty? Now, of course, it is easy to do so informally, I just asked you to visualize one. But what is a formal property the empty glass satisfies, that non-empty glasses do not?
The key idea here will be to define an additional operation to combine two glasses. We will call this operation pour, and define it as taking two glasses and pouring their contents into a new identical container.
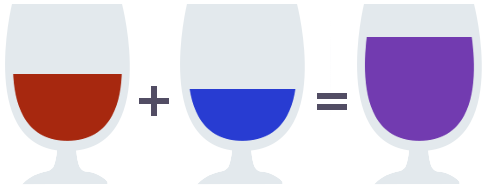
Equipped with this operation, we can find a property fulfilled by the empty glass and the empty glass alone: Pouring the contents of the empty glass into another glass leaves the other glass unchanged.

and similarly, pouring the contents of any glass into the empty glass
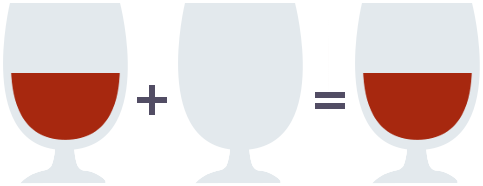
Formally, we can write this as the following pair of equations, where
x represents any arbitrary glass.
pour(emptyGlass, x) = x
pour(x, emptyGlass) = x
Definition
We can now take a look our other “empty” values, and check if they satisfy similar properties. And in fact, we will see that they do.
Take the number 0. To say that 0 is in our sense empty, we will
need to find an operation such that the equations above hold. We will
take the operation add, which adds two numbers together, i.e. the
operation such that add(3, 9) = 12. Now, it’s clear that
add(0, x) = x
add(x, 0) = x
so the value 0 is in fact empty according to our definition. In
particular we say that 0 is the identity element with respect to the
addition operation.
What about the empty array, or the empty string? We’ll kill two
birds with one stone. Define the operation concat, such
that concat("foo", "bar") = "foobar", and concat([1,2,3], [4,5]) = [1,2,3,4,5]. Then
concat("", x) = x
concat(x, "") = x
and
concat([], x) = x
concat(x, []) = x
The empty array, and the empty string, are identity elements with respect to their concatenation operations, and so their emptiness can be formally described.
In general we say that for a set A with a closed binary operation ⊕,
an empty (identity) element e is an element in A such that for all
x in A we have
x ⊕ e = x
e ⊕ x = x
Additional Examples
We could go on all day finding examples of identity elements, they are quite common, and there are plenty hiding in the wild. Let’s look at couple more.
First, let’s continue in the domain of numbers. We’ll take another
special value: infinity, or ∞. Infinity might seems like the
opposite of “empty”, but it will turn out to be an example of an
identity element. How exactly can we say that infinity is an empty
element of the numbers?
To understand this, think of upper bounds. Let’s say I make the statement, “The oldest person in the room is at most 80 years old”. This means I claim to have some information about how old the people in the room are. But what if I had absolutely no clue? One way to express this could be saying “The oldest person in the room is at most ∞ years old”.
Infinity, seen as an upper bound, conveys no information, and is thus
in this sense empty. What operation should we choose to express
this notion? The answer is to use the min operator.
min(∞, x) = x;
min(x, ∞) = x;
Exercise Make a similar argument for negative infinity, and choose a suitable operation to prove it’s “emptiness”.
Note that this means that for a given domain, multiple empty objects
may exist, with different choices of operators to give meaning to a
specific sense of emptiness. Another value we can choose is 1 with
the operation mul, such that mul(5,3) = 15.
mul(1, x) = x;
mul(x, 1) = x;
This interpretation of emptiness is combinatorial in nature.
Another important example is the identity function, (x => x), or
id as it’s often called. The identity function is the function that
takes an input and returns it unchanged. That is id(3) = 3, or
generally, id(x) = x
What operation could we choose to see that this is an identity
element? The operators we’re interested in are usually some natural
way of composing two elements, so the answer of course, is to choose
function composition: (f, g) => x => f(g(x)), or as it is often
written, the operator ∘. We then get the equations
f ∘ id = f
id ∘ f = f
This simply states that to process either the input or the output of a function by applying the identity function is a no-op.
If you ever wondered where the identity function derives its name
from, we see it is because it’s an identity element with respect to
function composition ∘.
Applications
The key to making practical use of the identity element pattern is usually to simply recognize that such an element exists, or on occasion choosing a model so that such an element can be found, for instance using forests over trees.
Consider the build system gulp, where we can describe a build step
to minify our code base in production mode only with the following
definition.
const optimize = env.production
? minify()
: util.noop();
gulp.task('build', () => {
return browserify(source).pipe(optimize);
});
We describe our optimization step as the stream processor minify, if
our environment is configured to production, and to the identity
element for the operation pipe, named util.noop, otherwise.
A no-op might seem like a useless build step, but we can see this code elegantly avoids awkward if-statements in the build task itself, delegating the responsibility of disabling optimizations to the optimization task.
If we were to design a build system ourselves, adding a no-op might not be an obvious inclusion, but equipped with understanding of the identity element pattern we can more easily identify its value.
